Comments(about)

Breaking away from the unnatural bond of circular symmetry was no easy task for Kepler. For he was shaken at being compelled to abandon a circular orbit and to question his faith in the Divine Geometer. Having cleared the stable of astronomy of circles and spirals, he was left, he said, with 'only a single cartful of dung' a stretched out circle something like an oval¹

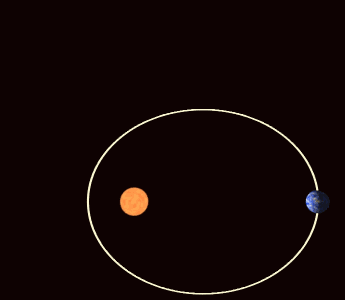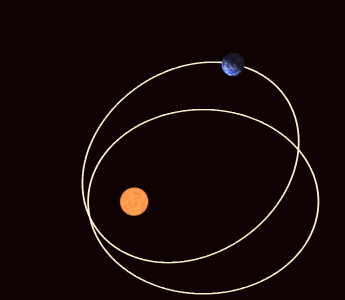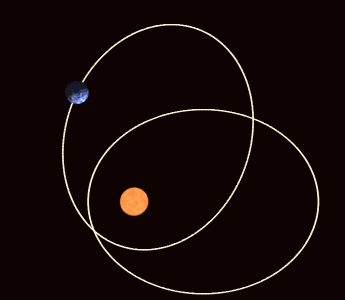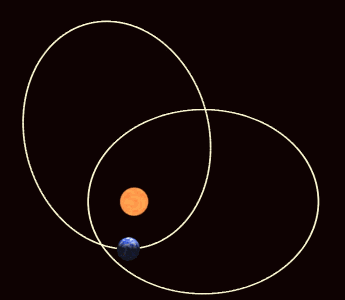
The elliptic orbit of a planet is a short-term description of a long-term trajectory of the planet that approximates to an ellipse rotating about the Sun as the exaggerated animation below shows. More precisely, the Sun and planets are together rotating in a state of balance about a pivot which is just a point in 'empty' spacetime. We shall see in due course that the ultimate pivot of physical balance is a point not even in empty spacetime, let alone in matter, but somewhere else as spacetime and matter are themselves constituents of the ultimate architecture of the physical world.

1. Carl Sagan, Cosmos, Macdonald & Co(Publishers)Ltd, Maxwell House, London EC2A 2EN, 1981, p 62.

Symmetry was first defined by Hermann Weyl, and this definition effectively means 'invariance under operation'. Accordingly, a symmetry property of a system is one that remains invariant under an operation (sometimes called a transformation) performed on the system. Figure 1, below, is a schematic illustration of symmetry operation.

As a special case, symmetry property can be the system itself; the simplest example of this case is the plane circle, as it remains unchanged if rotated arbitrarily about the perpendicular axis through its centre. Note that 'symmetry property' and 'operation' belong together, which means that each type of operation defines its own kind of symmetry. For example, everyday use of objects is a type of operation that leaves most of these objects approximately invariant, or constantly recognisable; hence, in everyday life symmetry objects of an approximate kind surround us.

Above definition of symmetry is too general to serve as an analytical tool in physics. However, in conjunction with Group Theory symmetry operations form a group with considerable analytical power. A fundamental feature of this group is the reversibility, or the invertibility, of operation that, strangely enough, gives the concept of 'operation' an antisymmetric character. Thus the symmetry group of operations itself is contingent on the state of inseparability between symmetry and antisymmetry. However, they are not present on an equal footing as a given symmetry feature is the result of a pair of arbitrary antisymmetry operations. That inequality is both the strength and the fundamental weakness of the Symmetry Group. An example of its strength is its ability to endow a particle of matter with an arbitrary linear velocity of an invariant magnitude. In other words, Symmetry Group enables us to theorise a particle of matter linearly moving anyhow in spacetime. However, this ability comes at a price; the price of decoupling of boost and rotation, in simpler language, decoupling of linear and rotary motions, in still simpler language, decoupling of spacetime and matter.

Symmetry or antisymmetry, just by itself unconditionally, is not in the field of human experience. What system of objects in the material world possesses just symmetry or antisymmetry? According to Pauli Exclusion Principle, not even two coupled electrons are interchangeable and hence not symmetric under the operation of interchange, against what appears as obvious to common sense. Also a particle and its anti-particle are not antisymmetric as they have the same mass.

If symmetry and antisymmetry exist together on an equal footing, then among various symmetry operations, there has to be at least one operation that applies to both. Such an operation, indeed, does exist, and we encountered it as ‘interchange’ in the previous paragraph. If two entities, on interchange, remain invariant then they are in a state of symmetry with respect to the interchange operation, but if they become somehow inverted then they are in a state of antisymmetry. These two states are idealistic extremes and as a rule two entities are neither completely symmetric nor antisymmetric. Let t and v denote two isotypic fundamental physical entities. Then their symmetry and antisymmetry components under the simplest form of the interchange-operation of t and v are a (t + v) and ± b (t - v) respectively, where a and b are scaling factors. The simplest fundamental forms of t and v are the kinetic and the potential energies of a mechanical system and their symmetry and antisymmetry components are the Hamiltonian and the Lagrangian, respectively. We know that these are the true infrastructural components of a mechanical system and not t and v, but this latter is our only means of accessing the former.

Let us take this opportunity to discuss briefly symmetry and antisymmetry in relation to how they naturally occur in the physical world. Consider the four fundamental physical interactions, Gravitation, Electromagnetism, Strong and Weak. The first two are long-range interactions rooted in symmetric and antisymmetric tensor fields, respectively, of the remaining two short-range nuclear interactions, Weak and Electromagnetism merge at high energies of the order of 100 GeV, and Strong, owing to its insensitivity to charge, may exhibit a similar behaviour with Gravitation. Therefore, the field aspect of the physical world presents excellent evidence that Nature weaves her field-fabric of the physical world with just the two interlocking patterns of symmetry and antisymmetry.

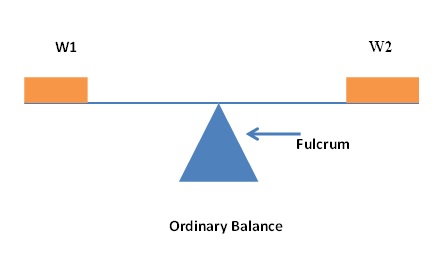
The two weights W1 and W2, at point of balance, are both equal to, say, W. Then one-half of their sum is W and one-half of their difference is zero. Therefore the symmetry measure, based on the operation of interchange of the two weights, is W and the antisymmetry measure, based on the same operation, is zero.

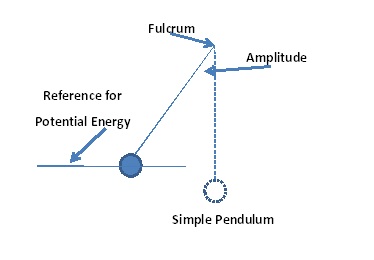
Now consider the simple pendulum, which is a case of dynamic balance between the kinetic and potential energies T and V of the pendulum bob. These energies are the counterparts of W1 and W2 that we considered above in relation to pure static balance. Potential energy V depends on a zero-reference level that we can set arbitrarily. Let us choose this level to be the highest point reached by the pendulum bob. This choice is unique for the following reason. Kinetic energy of the pendulum does not depend on the potential reference. It is completely independent of it. The choice we made for the potential reference equates potential energy to that kinetic energy and hence in that sense the choice is unique. With this unique choice, the simple pendulum becomes a model of pure dynamic balance. We now have, T = K and V = - K where K varies from zero to a maximum K_mwhich occurs when the pendulum bob is at its lowest point. The symmetry measure of T and V, which is (T + V)/2, is zero and the antisymmetry measure, which is ± (T - V)/2, works out to ± K; therefore the energies are in a state of pure antisymmetry.

For small oscillations, K_m is proportional to the product of the length of the string and the square of the amplitude of oscillation. However, according to quantum mechanics, energy of an oscillatory motion does not depend on the amplitudes, but depends only on the frequencies involved. The simple pendulum also simulates this quantum mechanical condition if we allow the pendulum length to vary freely, but infinitesimally slowly to keep this variation decoupled from the pendulum swing. The precise mathematical analysis of this dual motion is available on pages 114 and 115 of Max Born's book, Atomic Physics (Blackie & Son Limited, 1972).

Proper physical balance exhibits features of both pure static and pure dynamic balance that we discussed, above. In each of these two cases, the magnitudes of the two entities in balance are the same. Let us call it the Equality Condition. In the pure dynamic balance two orthogonal motions are present, one oscillatory and the other linear (such a dual motion, albeit trivial, is present in the pure static balance also). Let us refer to it as the Orthogonality condition. For the pure static balance, the antisymmetry measure of the two entities in balance is zero, and for the pure dynamic balance, the symmetry measure is zero. Let us label each of these as the Null condition.

Equality Orthogonality and Nullity ( more accurately Null Singularity) that we referred to above are all necessary conditions of proper physical balance. They may also be sufficient.

In the physical world, from a practical and observational point of view, the primary pair of physical entities in balance is the pair of vectors that represent the linear and the angular motions of a fundamental particle of matter. If these two vectors are a and b, then according to the first of the above three conditions, their magnitudes are equal. According to the second condition, their scalar product ab is zero. Finally, according to the third, the magnitudes of the vectors (a + b) and ± (a - b) are also zero.

However, the triple criteria of balance are satisfied not only by the pair, linear and angular, but also by each of the remaining two pairs of the triple pair-formation

Field- Particle

Spacetime - Matter

of the physical world that we encountered in the About page.

In static balance, fulcrum is in a passive role. In dynamic balance, we found that there is activity at the pivotal point due to varying pendulum length. Therefore, there is room to think that the fulcrum in dynamic balance is in a reasonably active role. In the real physical world, this involvement of the fulcrum is at an extreme and is quite complex and deep. The pivot end of this fulcrum is what we perceive presently as the Microwave Background radiation and the rest of the fulcrum is perhaps Dark Energy.

There is an elegant real-life example that illustrates this complexity and depth quite effectively. Consider the final of a grand slam tennis match such as that epic battle between the tennis supremos Nadal and Federer at Wimbledon in 2008. In such situations players, without doubt, satisfy the Equality criterion. They are free to act independently and yet they remain connected via the tennis ball; therefore, the act of playing tennis is one of relative freedom, as in Orthogonality. At a grand slam final, the outcome of the match is contingent on mental agility rather than on physical strength. In other words, the players occupy a plane of reality on which it is the mind and not the body that is at play; hence, they also satisfy the criterion of physical Nullity.

Even with the triple criteria satisfied, the match has no meaning without the complex infrastructure consisting of a well-constructed tennis court, an umpire, line judges, ball boys and girls and hawk eye and other similar high-tech devices. In the language of balance, all these collectively represent the fulcrum, which, on occasion, is even able to tip the balance in favour of one player or the other.

One of the most famous parables told by the Buddha is the Parable of the Raft. In this he likened his teachings to a raft for crossing a fast-flowing river.

The parable narrates how a man is trapped on one side of a river. On this side, there is great danger and uncertainty and on the far side of the river is safety. However there is no bridge spanning the river nor is there a ferry to cross over. What to do? The man gathers together logs, leaves, and creepers and by his wit fashions a raft from these materials. By lying on the raft and using his hands and feet as paddles he manages to cross the river from the dangerous side to the side of safety.

The Buddha then asks the listeners a question. What would you think if the man, having crossed over the river thought to himself – That raft has served me well I will carry it on my back over the land now? The monks replied that it would not be a very sensible idea to cling to the raft in such a way. The Buddha went on – What if he lay the raft down gratefully thinking that this raft has served him well but is no longer of use and can thus be laid down upon the shore? The monks replied that this would be the proper attitude. The Buddha concluded by saying – So it is with my teachings which are like a raft and are for crossing over with not for seizing hold of.

This parable marks the attitude taken to the teachings given by the Buddha, firstly that their prime objective is to be of practical use and secondly to introduce the teaching of the Two Truths. The ultimate Truth or Reality cannot be described by words and concepts and must be seen for oneself. However the path that leads to that insight can be described and forms a map to show how to get there. This truth is relative because it only describes the way to this Truth it is not the Truth itself nor is it the path itself. The Buddhist practitioner must walk this path; it is not enough just to read about it or even to believe that it works!

Thus we must always bear in mind that the teachings, even the story of the Life of the Buddha are only descriptions, symbols pointing to something beyond the words and neither must they be taken as scientific fact or even historical truths.

This is why it is futile to become bogged down in ontological or epistemological arguments over these teachings. The value of them is realised when they are used in the way they were designed to be used as a practical tool leading toward insight into the human condition.